


Next: Example
Up: No Title
Previous: No Title
Recall that for the Euler method we showed that the local truncation error is
proportional to 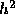 and that for a finite interval the global
truncation error is at most a constant times h. In general, for a method of
order p, the local truncation error is proportional to
and that for a finite interval the global
truncation error is at most a constant times h. In general, for a method of
order p, the local truncation error is proportional to 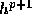 and the
global truncation error on a finite interval is bounded by a constant times
and the
global truncation error on a finite interval is bounded by a constant times
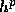 . To achieve high accuracy we normally use a numerical procedure for
which p is fairly large, perhaps four or higher. As p increases, the
formula used in computing
. To achieve high accuracy we normally use a numerical procedure for
which p is fairly large, perhaps four or higher. As p increases, the
formula used in computing 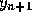 normally becomes more complicated and
hence more calculations are required at each step; however, this is
usually not a serious problem unless
normally becomes more complicated and
hence more calculations are required at each step; however, this is
usually not a serious problem unless 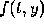 is very complicated or the
calculation must be repeated very many times. If the step size h is
decreased, the global truncation error is decreased by the same factor raised
to the power p. However, as we mentioned earlier, if h is very small,
a great many steps will be required to cover a fixed
interval, and the global round-off error may be larger than the global
truncation error. We assume that the round-off error
is very complicated or the
calculation must be repeated very many times. If the step size h is
decreased, the global truncation error is decreased by the same factor raised
to the power p. However, as we mentioned earlier, if h is very small,
a great many steps will be required to cover a fixed
interval, and the global round-off error may be larger than the global
truncation error. We assume that the round-off error
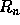 is proportional to the number of computations performed and therefore
is inversely proportional to a positive power of h. We know
that the total error is bounded by
is proportional to the number of computations performed and therefore
is inversely proportional to a positive power of h. We know
that the total error is bounded by  ; hence we wish to
choose h so as to minimize this quantity. The optimum value of h occurs
when the rate of increase of the truncation error (as h increases) is
balanced by the rate of decrease of the round-off error.
; hence we wish to
choose h so as to minimize this quantity. The optimum value of h occurs
when the rate of increase of the truncation error (as h increases) is
balanced by the rate of decrease of the round-off error.
Dinesh Manocha
Sat Apr 4 20:31:47 EST 1998
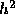 and that for a finite interval the global
truncation error is at most a constant times h. In general, for a method of
order p, the local truncation error is proportional to
and that for a finite interval the global
truncation error is at most a constant times h. In general, for a method of
order p, the local truncation error is proportional to 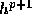 and the
global truncation error on a finite interval is bounded by a constant times
and the
global truncation error on a finite interval is bounded by a constant times
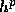 . To achieve high accuracy we normally use a numerical procedure for
which p is fairly large, perhaps four or higher. As p increases, the
formula used in computing
. To achieve high accuracy we normally use a numerical procedure for
which p is fairly large, perhaps four or higher. As p increases, the
formula used in computing 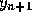 normally becomes more complicated and
hence more calculations are required at each step; however, this is
usually not a serious problem unless
normally becomes more complicated and
hence more calculations are required at each step; however, this is
usually not a serious problem unless 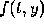 is very complicated or the
calculation must be repeated very many times. If the step size h is
decreased, the global truncation error is decreased by the same factor raised
to the power p. However, as we mentioned earlier, if h is very small,
a great many steps will be required to cover a fixed
interval, and the global round-off error may be larger than the global
truncation error. We assume that the round-off error
is very complicated or the
calculation must be repeated very many times. If the step size h is
decreased, the global truncation error is decreased by the same factor raised
to the power p. However, as we mentioned earlier, if h is very small,
a great many steps will be required to cover a fixed
interval, and the global round-off error may be larger than the global
truncation error. We assume that the round-off error
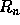 is proportional to the number of computations performed and therefore
is inversely proportional to a positive power of h. We know
that the total error is bounded by
is proportional to the number of computations performed and therefore
is inversely proportional to a positive power of h. We know
that the total error is bounded by  ; hence we wish to
choose h so as to minimize this quantity. The optimum value of h occurs
when the rate of increase of the truncation error (as h increases) is
balanced by the rate of decrease of the round-off error.
; hence we wish to
choose h so as to minimize this quantity. The optimum value of h occurs
when the rate of increase of the truncation error (as h increases) is
balanced by the rate of decrease of the round-off error.


