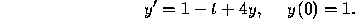



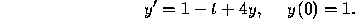
Using the Euler method with various step sizes, calculate approximate values
for the solution 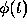 at
at 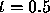 and t = 1. Try to determine
the optimum step size.
and t = 1. Try to determine
the optimum step size.
Keeping only four digits in order to shorten the calculations, we obtain the
data shown in Table 1. The first two columns are the step size
h and the number of steps N required to traverse the interval
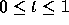 . Then
. Then 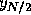 and
and 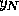 are approximations
to
are approximations
to  and
and 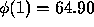 , respectively. These
quantities appear in the third and fifth columns.
The fourth and sixth columns display the differences between the calculated
values and the actual value of the solution.
, respectively. These
quantities appear in the third and fifth columns.
The fourth and sixth columns display the differences between the calculated
values and the actual value of the solution.
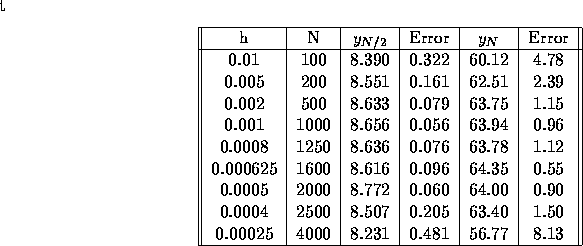
Table 1: Approximations to the Solution of the Initial Value Problem,
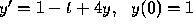 , using the
Euler Method with Different Step Sizes
, using the
Euler Method with Different Step Sizes
For relatively large step sizes the round-off error is much less than the
global truncation error. Consequently, the total error is approximately
the same as the global truncation error, which for the Euler method is bounded
by a constant times h. Thus, as the step size is reduced, the error is
reduced proportionally. The first three lines in Table 1
show this type of behavior. For 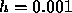 the error has been further
reduced, but much less than proportionally; this indicates that round-off
error is becoming important. As h is reduced still more the error begins
to fluctuate and further improvements in accuracy become problematical.
For values of h less than
the error has been further
reduced, but much less than proportionally; this indicates that round-off
error is becoming important. As h is reduced still more the error begins
to fluctuate and further improvements in accuracy become problematical.
For values of h less than 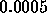 the error is clearly increasing,
which indicates that round-off error is now the dominant part
of the total error.
the error is clearly increasing,
which indicates that round-off error is now the dominant part
of the total error.
These results can also be expressed in terms of the number of steps N.
For N less than about 1000 accuracy is improved by taking more steps, while
for N greater than about 2000 using more steps has an adverse effect.
Thus for this problem it is best to use an N somewhere between 1000 and
2000. For the calculations shown in Table 1 the best result
at 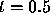 occurs for N = 1000 while at
occurs for N = 1000 while at 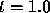 the best result is
for N = 1600.
the best result is
for N = 1600.


