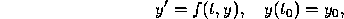



In previous sections we have discussed numerical procedures for solving the initial value problem
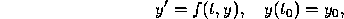
in which data at the point 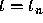 are used to calculate an approximate
value of the solution
are used to calculate an approximate
value of the solution 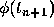 at the next mesh point
at the next mesh point
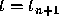 . In other words, the calculated value of
. In other words, the calculated value of 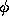 at any mesh
point depends only on the data at the preceding mesh pont. Such methods are
called one-step methods. However, once approximate values of the
solution
at any mesh
point depends only on the data at the preceding mesh pont. Such methods are
called one-step methods. However, once approximate values of the
solution 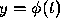 have been obtained at a few points
beyond
have been obtained at a few points
beyond 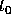 , it is natural to ask whether we can make use of some of this
information, rather than just the value at the last point to calculate the
value of
, it is natural to ask whether we can make use of some of this
information, rather than just the value at the last point to calculate the
value of 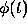 at the next point.
Specifically, if
at the next point.
Specifically, if  at
at 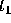 ,
,
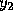 at
at 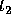 ,
,  ,
, 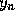 at
at 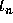 are known,
how can we use this information to determine
are known,
how can we use this information to determine 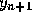 at
at 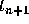 ?
Methods that use information at more than the last mesh point are referred to
as multistep methods. In this section we will describe two types of
multistep methods, Adams methods and backward differentiation formulas.
Within each type one can achieve various levels of accuracy, depending on the
number of preceding data points that are used. For simplicity we will assume
throughout our discussion that the step size h is
constant.
?
Methods that use information at more than the last mesh point are referred to
as multistep methods. In this section we will describe two types of
multistep methods, Adams methods and backward differentiation formulas.
Within each type one can achieve various levels of accuracy, depending on the
number of preceding data points that are used. For simplicity we will assume
throughout our discussion that the step size h is
constant.