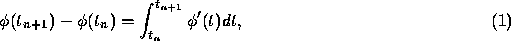



where 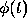 is the solution of the initial value problem. The basic idea
of an Adams method is to approximate
is the solution of the initial value problem. The basic idea
of an Adams method is to approximate 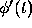 by a polynomial
by a polynomial
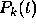 of degree k - 1 and to use the polynomial to evaluate the
integral on the right side of Eq. (1). The coefficients in
of degree k - 1 and to use the polynomial to evaluate the
integral on the right side of Eq. (1). The coefficients in
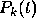 are determined by using previously calculated data
points. For example, suppose that we wish to use only the points
are determined by using previously calculated data
points. For example, suppose that we wish to use only the points
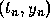 and
and 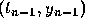 . Then the polynomial
. Then the polynomial 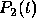 is
of degree one and has the form
is
of degree one and has the form  . Since
. Since 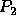 is to be an
approximation to
is to be an
approximation to 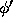 , we require that
, we require that 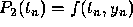 and that
and that 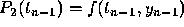 . Recall that we denote
. Recall that we denote
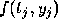 by
by 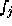 for an integer j. Then A and B must satisfy
the equations
for an integer j. Then A and B must satisfy
the equations


Solving for A and B, we obtain
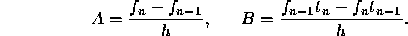
Replacing 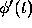 by
by 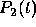 and evaluating the integral
in Eq. (1), we find that
and evaluating the integral
in Eq. (1), we find that
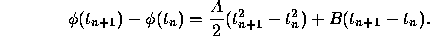
Finally, we replace 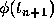 and
and 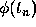 by
by 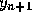 and
and
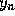 , respectively, and carry out some algebraic simplification.
For a constant step size h we obtain
, respectively, and carry out some algebraic simplification.
For a constant step size h we obtain
Equation (2) is the second order Adams-Bashforth formula.
It is an explicit formula for 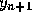 in terms of
in terms of 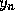 and
and 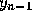 and has a local truncation error proportional to
and has a local truncation error proportional to 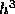 .
.
We note in passing that the first order Adams-Bashforth formula, based on the
polynomial 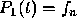 of degree zero, is just the original
Euler formula.
of degree zero, is just the original
Euler formula.
More accurate Adams formulas can be obtained by following the procedure
outlined above, but using a higher degree polynomial and correspondingly more
data points. For example, suppose that a polynomial 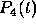 of degree
three is used. The coefficients are determined from the four points
of degree
three is used. The coefficients are determined from the four points
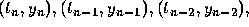 and
and 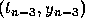 . Substituting this polynomial for
. Substituting this polynomial for
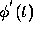 in Eq. (1), evaluating the integral, and simplifying the
result, we eventually obtain the fourth order Adams-Bashforth formula,
namely,
in Eq. (1), evaluating the integral, and simplifying the
result, we eventually obtain the fourth order Adams-Bashforth formula,
namely,
The local truncation error of this fourth order formula is proportional
to 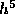 .
.
A variation on the derivation of the Adams-Bashforth formulas gives another set
of formulas called the Adams-Moulton formulas. To see the difference, let
us again consider the second order case. Again we use a first degree
polynomial 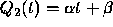 , but we determine the coefficients by
using the points
, but we determine the coefficients by
using the points 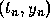 and
and 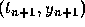 .
Thus
.
Thus 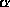 and
and 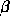 must satisfy
must satisfy


and it follows that
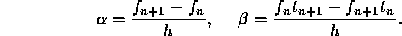
Substituting 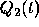 for
for 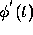 in Eq. (1) and simplifying,
we obtain
in Eq. (1) and simplifying,
we obtain
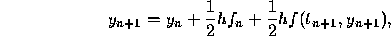
which is the second order Adams-Moulton formula. We have written
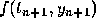 in the last term to emphasize that the
Adams-Moulton formula is implicit, rather
than explicit, since the unknown
in the last term to emphasize that the
Adams-Moulton formula is implicit, rather
than explicit, since the unknown 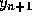 appears on both sides of the
equation. The local truncation error for the second order Adams-Moulton
formula is proportional to
appears on both sides of the
equation. The local truncation error for the second order Adams-Moulton
formula is proportional to 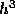 .
.
The first order Adams-Moulton formula is just the backward Euler formula, as you might anticipate by analogy with the first order Adams-Bashforth formula.
More accurate higher order formulas can be obtained by using an approximating
polynomial of higher degree. The fourth order Adams-Moulton formula, with a
local truncation error porportional to 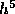 , is
, is
Observe that this is also an implicit formula because 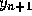 appears in
appears in
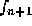 .
.
Although both the Adams-Bashforth and Adams-Moulton formulas of the same order have local truncation errors proportional to the same power of h, the Adams-Moulton formulas of moderate order are in fact considerably more accurate. For example, for the fourth order formulas (3) and (4), the proportionality constant for the Adams-Moulton formula is less than 1/10 of the proportionality constant for the Adams-Bashforth formula. Thus the question arises: should one use the explicit (and faster) Adams-Bashforth formula, or the more accurate but implicit (and slower) Adams-Moulton formula? The answer depends on whether by using the more accurate formula one can increase the step size, and therefore reduce the number of steps enough to compensate for the additional computations required at each step.
In fact, numerical analysts have attempted to achieve both simplicity and
accuracy by combining the two formulas in what is called a
predictor-corrector method. Once 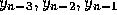 , and
, and
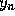 are known we can compute
are known we can compute 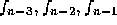 , and
, and 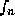 ,
and then use the Adams-Bashforth (predictor) formula (3) to
obtain a first value for
,
and then use the Adams-Bashforth (predictor) formula (3) to
obtain a first value for 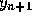 . Then we compute
. Then we compute 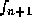 and use the
Adams-Moulton (corrector) formula (4), which is no longer implicit,
to obtain an improved value of
and use the
Adams-Moulton (corrector) formula (4), which is no longer implicit,
to obtain an improved value of 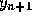 . We can, of course, continue to
use the corrector formula (4) if the
change in
. We can, of course, continue to
use the corrector formula (4) if the
change in  is too large. However, if it is necessary to use the
corrector formula more than once or perhaps twice, it means that the step size
h is too large and should be reduced.
is too large. However, if it is necessary to use the
corrector formula more than once or perhaps twice, it means that the step size
h is too large and should be reduced.
In order to use any of the multistep methods it is necessary first to
calculate a few 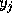 by some other method. For example, the fourth order
Adams-Moulton method requires values for
by some other method. For example, the fourth order
Adams-Moulton method requires values for 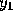 and
and 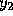 , while the fourth
order Adams-Bashforth method also requires a value for
, while the fourth
order Adams-Bashforth method also requires a value for 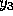 . One way to
proceed is to use a one-step method of comparable accuracy to calculate the
necessary starting values. Thus, for a fourth order multistep method, one
might use the fourth order Runge-Kutta method to calculate the
starting values.
. One way to
proceed is to use a one-step method of comparable accuracy to calculate the
necessary starting values. Thus, for a fourth order multistep method, one
might use the fourth order Runge-Kutta method to calculate the
starting values.
Another approach is to use a low order method with a very small h to
calculate 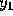 and then to increase gradually both the order and the step
size until enough starting values have been determined.
and then to increase gradually both the order and the step
size until enough starting values have been determined.


