 to
approximate the solution
to
approximate the solution 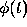 of the initial value problem rather than
its derivative
of the initial value problem rather than
its derivative 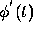 , as in the Adams methods. We them
differentiate
, as in the Adams methods. We them
differentiate 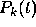 and set
and set 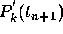 equal to
equal to 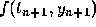 to obtain an implicit formula for
to obtain an implicit formula for 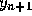 . These are called
backward differentiation formulas.
. These are called
backward differentiation formulas.



Another type of multistep method arises by using a polynomial  to
approximate the solution
to
approximate the solution 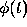 of the initial value problem rather than
its derivative
of the initial value problem rather than
its derivative 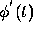 , as in the Adams methods. We them
differentiate
, as in the Adams methods. We them
differentiate 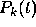 and set
and set 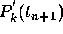 equal to
equal to 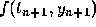 to obtain an implicit formula for
to obtain an implicit formula for 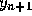 . These are called
backward differentiation formulas.
. These are called
backward differentiation formulas.
The simplest case uses a first degree polynomial  . The
coefficients are chosen to match the computed values of the solution
. The
coefficients are chosen to match the computed values of the solution
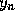 and
and 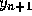 . Thus A and B must satisfy
. Thus A and B must satisfy
Since 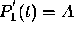 , the requirement that
, the requirement that
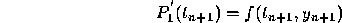
is just
Another expression for A comes from subtracting the first of Eqs. (5) from the second, which gives

Substituting this value of A into Eq. (6) and rearranging terms, we obtain the first order backward differentiation formula
Note that this equation is the backward Euler formula, we had seen earlier.
By using higher order polynomials and correspondingly more data point one can obtain backward differentiation formulas of any order. The second order formula is
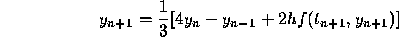
and the fourth order formula is
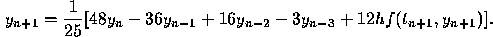
These formulas have local truncation error proportional to 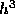 and
and 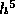 ,
respectively.
,
respectively.