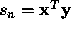 , where
, where
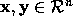 . Since the order of evaluation of
. Since the order of evaluation of
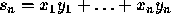 affects the analysis (but not the
final error bound), we will assume that the evaluation is from left
to right.
affects the analysis (but not the
final error bound), we will assume that the evaluation is from left
to right.
Consider the dot product of two vectors, 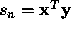 , where
, where
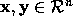 . Since the order of evaluation of
. Since the order of evaluation of
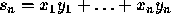 affects the analysis (but not the
final error bound), we will assume that the evaluation is from left
to right.
affects the analysis (but not the
final error bound), we will assume that the evaluation is from left
to right.
Let 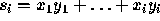 denote the ith partial sum. Using
the IEEE error model, we have
denote the ith partial sum. Using
the IEEE error model, we have
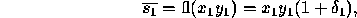
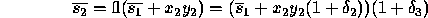
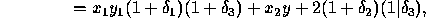
where 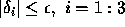 . For our analysis we will not
differentiate between the different
. For our analysis we will not
differentiate between the different 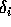 , so to simplify the
expressions let us drop the subscripts on the
, so to simplify the
expressions let us drop the subscripts on the 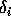 and write
and write
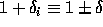 . Then
. Then
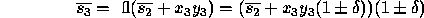
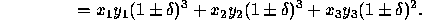
Based on this pattern, we have
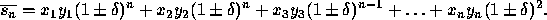
There are various ways to simplify this result. In particular, we make use of the following lemma:
Lemma
If
where
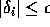 and
and 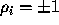 for
for 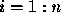 , and
, and 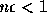 , then
, then
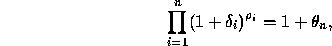

Applying the lemma to 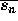 , we obtain
, we obtain
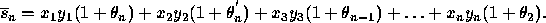
This is backward error results and may be interpreted as follows: the
computed inner product is the exact one for a perturbed set of data
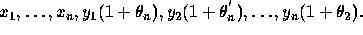 Each perturbation is ``small".
Each perturbation is ``small".