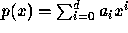 . We use
Horner's rule, given as:
. We use
Horner's rule, given as:
Goal: Evaluate a polynomial 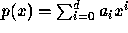 . We use
Horner's rule, given as:
. We use
Horner's rule, given as:
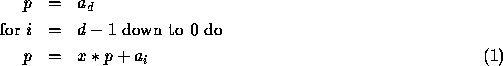
Lets apply it to 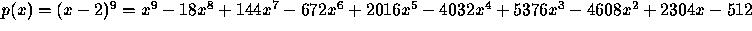 .
.
What would happen if we tried to find a zero of 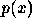 using a simple
zero finder? The root finder is based on the bisection algorithm:
using a simple
zero finder? The root finder is based on the bisection algorithm:
function bisect(xl, xu, tol, p)
/* find a zero of p(x) in [xl, xu] assuming p(xl) . p(xu) < 0 */
/* stop if zero found to within +/- tol */
if (xu-xl) <= (2 * tol)
return ((xl + xu)/2)
else
mid = (xl + xu)/2
pm = p(mid) /* the polynomial P(x) is evaluated a x = mid */
if p(xl) . pm < 0 then
return bisect(xl,mid,tol,p)
else
return bisect(mid xu,tol,p)
endif
endif
Let us apply to 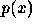 with
with 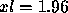 to
to 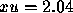 . What
will happen? Look at the graphs of
. What
will happen? Look at the graphs of 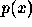 shown in Fig. 4 and
Fig. 5.
shown in Fig. 4 and
Fig. 5.
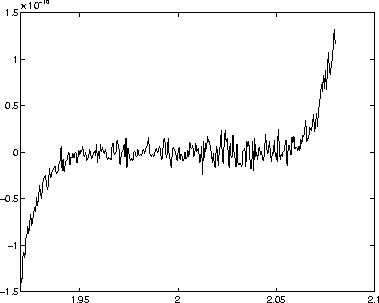
Figure 5: Graph of 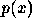 in the neighborhood of x =2 evaluated using IEEE
double precision arithmetic
in the neighborhood of x =2 evaluated using IEEE
double precision arithmetic