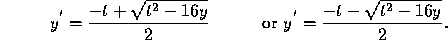The order of a differential equation is the order of the highest derivative that appears in the equation. Thus Eqs. (1) and (2) are second order ordinary differential equations, and Eq. (3) is a first order ordinary differential equation. Equations (4), (5), and (6) are second order partial differential equations. More generally, the equation
is an ordinary differential equation of the nth order. Equation (8)
represents a relation between the independent variable t and the
values of the function u and its first n derivatives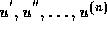 
. It is convenient and customary in
differential equations to write y for 
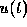, with 
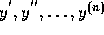standing for 
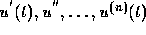. Thus Eq. (8) is written as
For example,
is a third order differential equation for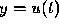 
. Occasionally,
other letters will be used instead of t and y for the independent and
dependent variables; the meaning should be clear from the context.
Furthermore, we would assume that it is always possible to solve a given ordinary differential equation for the highest derivative, obtaining
We study only equations of the form (11). This is mainly to avoid the ambiguity that may arise because a single equation of the form (9) may correspond to several equations of the form (11). For example, the equation
leads to the two equations
