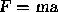 . If
. If 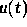 is the
position at time
is the
position at time 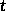 of a particle of mass
of a particle of mass 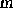 acted on by a
force
acted on by a
force 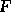 , then we obtain
, then we obtain



Many important and significant problems in engineering, the physical
sciences, and the social sciences, when formulated in mathematical
terms, require the determination of a function satisfying an equation
containing one or more derivatives of the unknown function. Such
equations are called differential equations. The most
familiar example is Newton's law 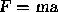 . If
. If 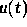 is the
position at time
is the
position at time 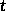 of a particle of mass
of a particle of mass 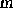 acted on by a
force
acted on by a
force 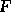 , then we obtain
, then we obtain
where the force 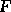 may be a function of t,u, and the
velocity
may be a function of t,u, and the
velocity 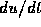 . To determine the motion of a particle subject to a
given force F it is necessary to find a function u satisfying the
differential equation (1).
. To determine the motion of a particle subject to a
given force F it is necessary to find a function u satisfying the
differential equation (1).
The main purpose of this course is to discuss numerical approaches to solve these differential equations. In many real-world cases, the differential equations do not have a closed form solution. We start with a review of some of the terminology.