 is a function
is a function 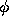 such that
such that
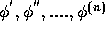 exist and satisfy
exist and satisfy



A solution of the ordinary differential equation (11)
on the interval  is a function
is a function 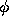 such that
such that
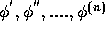 exist and satisfy
exist and satisfy
for every t in 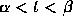 . Unless stated otherwise, we
assume that the function f of Eq. (11) is a real-valued function,
and we are interested in obtaining real-valued solutions
. Unless stated otherwise, we
assume that the function f of Eq. (11) is a real-valued function,
and we are interested in obtaining real-valued solutions 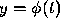 .
.
It is easily verified by direct substitution that the first order equation (3),

has the solution
where c is an arbitrary constant.
Although for the equation (3), we are
able to verify that certain simple functions are
solutions, in general we do not have such solutions readily available.
Thus a fundamental question is the following: Does an equation of the
form (11) always have a solution? The answer is "NO."
Merely writing down an equation of the form (11) does not necessarily
mean that there is a function 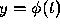 that satisfies it.
So, how can we tell whether some particular equation has a solution?
This is the question of existence of a solution, and it is not a purely
mathematical concern, for at least two reasons.
that satisfies it.
So, how can we tell whether some particular equation has a solution?
This is the question of existence of a solution, and it is not a purely
mathematical concern, for at least two reasons.
A more practical concern is: given a differential equation of the form (11), can we actually detemine a solution, and if so, how? Note that if we find a solution of the given equation, we have at the same time answered the question of the existence of a solution. However, without knowledge of existence theory we might, for example, use a computer to find a numerical approximation to a "solution" that does not exist. On the other hand, even though we may know that a solution exists, it may be that the solution is not expressible in terms of the usual elementary functions---polynomial, trigonometric, exponential, logarithmic, and hyperbolic functions. Unfortunately, this is the situation for most differential equations arising in scientific applications.


