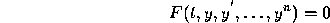
A crucial classification of differential equations is according to whether they are linear or nonlinear. The ordinary differential equation
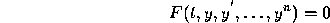
is said to be linear if F is a linear function of the variables
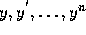: a similar definition applies to parital
differential
equations. Thus the general linear ordinary differential equation of order
n is
Equations (2) through (6)are linear equations. An
equation that is not of the form (14) is a nonlinear equation.
Equation (10) is nonlinear because of the term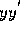 
.
A simple physical problem that leads to a nonlinear differential equation is
the oscillating pendulum. The angle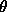 
that an oscillating pendulum
of length L makes with the vertical direction
satisifies the nonlinear equation
The mathematical theory and the methods for solving linear equations
are highly developed. In contrast, for nonlinear equations the theory is
more complicated and methods of solution are less satisfactory. In view
of this it is fortunate that many significant problems lead to linear
ordinary differential equations or, at least in the first approximation, to
linear equations. For example, for the pendulum, if the angle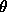 
is small, then 
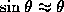and Eq. (15) can be
approximated by the linear equation
This process of approximation a nonlinear equation by a linear one is called linearization and it is an extremely valuable way to deal with nonlinear equations. Nevertheless, there are many physical phenomena that simply cannot be represented adequately by linear equations; to study these phenomena it is essential to deal with nonlinear equations. For most of this course, we will be dealing with linear differential equations. Furthermore, we would deal with two kind of problems:
